応用情報技術者試験に頻出するハッシュ法についてまとめました。
ハッシュ法
ハッシュ法とは
ハッシュ法とは、データ探索アルゴリズムの一種で、ハッシュ関数と呼ばれる計算式を使用して、データのアドレス(記憶場所の位置)を探索する方法です。
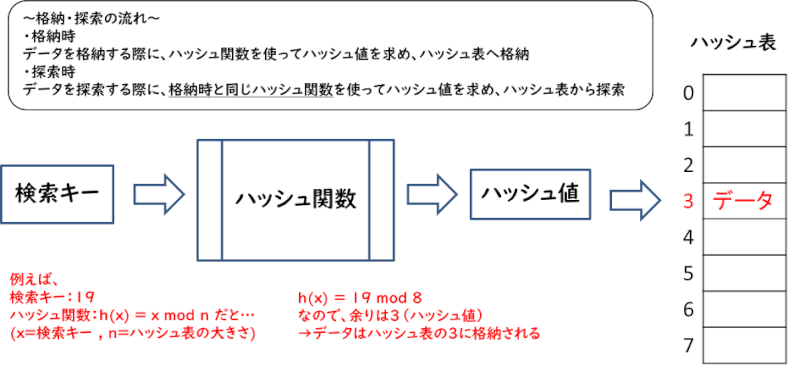
有名なハッシュ関数としてMD5やSHA256といったものがありますが、特にこれを使わなければならないという決まりはありません。
衝突・シノニムの発生
異なる検索キーで、ハッシュ関数を通した際に同じハッシュ値となる場合があり、このことを衝突(コリュジョン)、もしくはハッシュ値が同じ値になるのでシノニムの発生といいます。
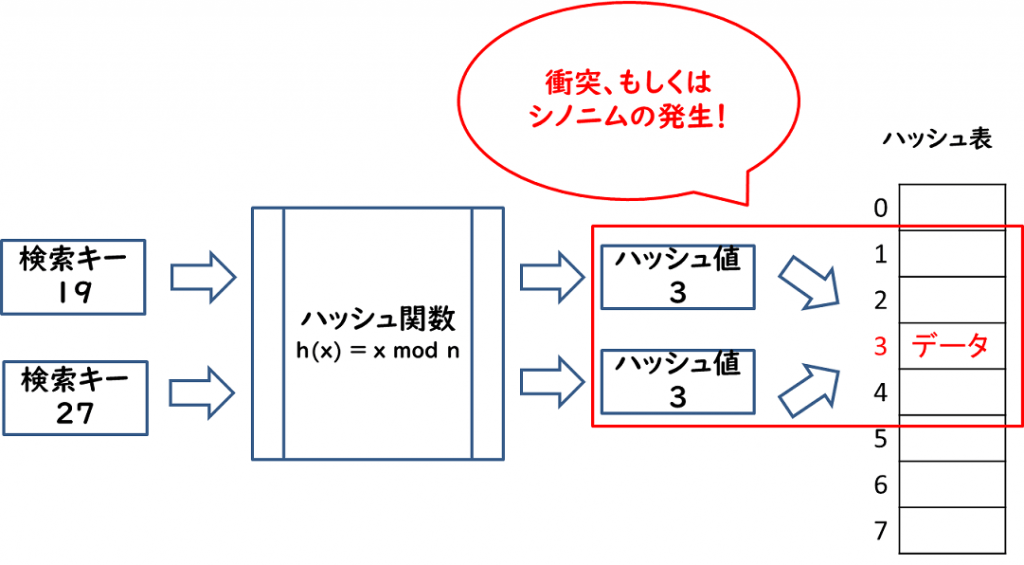
衝突への対処は、チェイン法やオープンアドレス法にて対応します。
・チェイン法
ハッシュ表にデータと一緒にポインタを持たせ、衝突の際は連結リストを用い格納していきます。
・オープンアドレス法
衝突の際は別のハッシュ関数を使用し再度ハッシュ値を求め、格納していきます。
演習問題
実際の試験の過去問を解いてみましょう。
応用情報技術者試験 令和元年秋期 午前問7 問題
| IPA 応用情報技術者試験(AP) 問題より 問7 自然数をキーとするデータを、ハッシュ表を用いて管理する。キーxのハッシュ関数h(x)を h(x) = x mod n とすると、任意のキーaとbが衝突する条件はどれか。ここで、nはハッシュ表の大きさであり、x mod nはxをnで割った余りを表す。 選択肢 ア a+bがnの倍数 イ a-bがnの倍数 ウ nがa+bの倍数 エ nがa-bの倍数 |
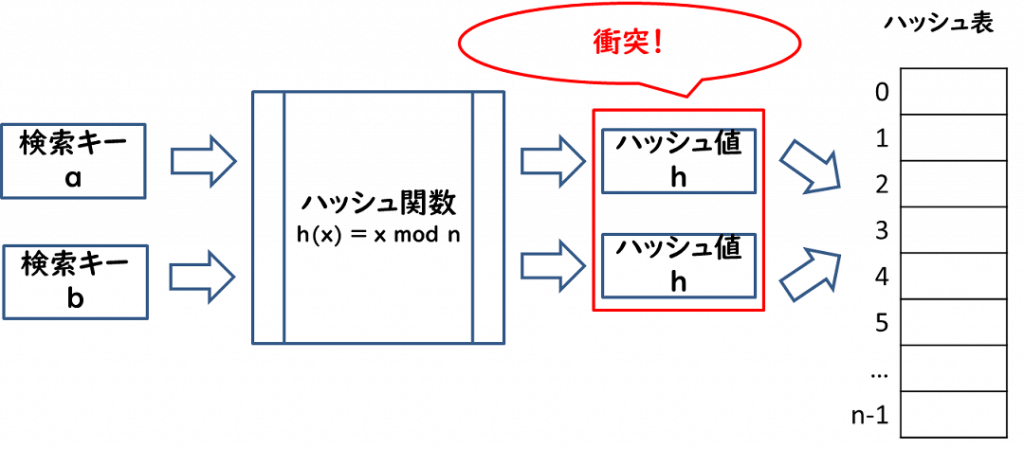
応用情報技術者試験 令和元年秋期 午前問7 解答
衝突する適当な値で、選択肢と合致するか試していきます。
| ① n = 8 aの場合、27 mod 8 = 3 bの場合、19 mod 8 = 3 ア a+bがnの倍数 (27+19)/8=5.75のため倍数ではない イ a-bがnの倍数 (27-19)/8=1のため倍数 ⇒ 合致! ウ nがa+bの倍数 8/(27+19)=0.17…のため倍数ではない エ nがa-bの倍数 8/(27-19)=1のため倍数 ⇒ 合致! |
ここで、「イ」と「エ」が残りますので、別パターンでも試してみます。
| ② n = 8 aの場合、 25 mod 5 = 0 bの場合、10 mod 5 = 0 イ a-bがnの倍数 (25-10)/5=3のため倍数 ⇒ 合致! エ nがa-bの倍数 5/(25-10)=0.33…のため倍数ではない |
以上から、答えは「イ」となります。
ハッシュ法の解説は以上です。
こちらに応用情報技術者試験の問題について、
解説を掲載していますので、良かったらご覧ください。
当ブログ「応用情報技術者解答解説」まとめページはこちら


