応用情報技術者試験に頻出する待ち行列理論についてまとめました。
待ち行列理論
待ち行列とは

待ち行列とは、何かしらの処理を待つ行列のことです。
例えば、レジに並ぶお客さんを想像していただくと良いかと思います。
待ち行列理論は、待ち行列に関する要素を確立的にモデル化し、「待ち時間」や「待ち行列の長さ」、「サービス時間」などを求めます。
M/M/1の待ち行列モデル
M/M/1とは、待ち行列の代表的なモデルの一つで
M:時間あたりの到着数がランダム
M:1件あたりのサービス時間がランダム
1:サービスを受ける窓口数が1つ
となります。
(Mは無記憶のMemorylessもしくはマルコフの Markovianの略語ですが、何故そうなのかを説明するとややこしくなるので、詳しく知りたい方はWiki:M/M/1 待ち行列を見てくださいね。M=ランダムと覚えてもらってもいいと思います)
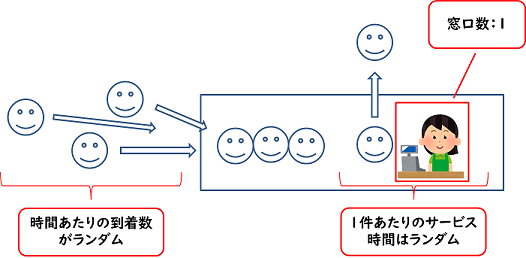
お店に例えると「1つのレジに対して不定期に人が来て行列を作り、人によって購入する商品数が違うのでそれぞれ異なる時間で対応する」ということです。
待ち行列の公式
代表的なものを紹介します。
まず、待ち行列の基本要素として
平均到着率(λ)、平均サービス率(μ)、利用率(ρ)
があり、
・平均到着間隔=1÷平均到着率(λ)
・平均サービス時間=1÷平均サービス率(μ)
・利用率(ρ)=平均サービス時間÷平均到着間隔=平均到着率(λ)÷平均サービス率(μ)
となります。
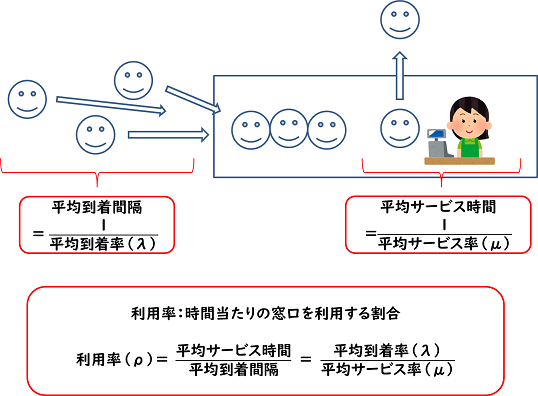
それら要素を使って、以下の公式があります。
・平均待ち時間=利用率(ρ)÷(1-利用率(ρ))×平均サービス時間(1÷μ)
・平均応答時間=平均待ち時間+平均サービス時間
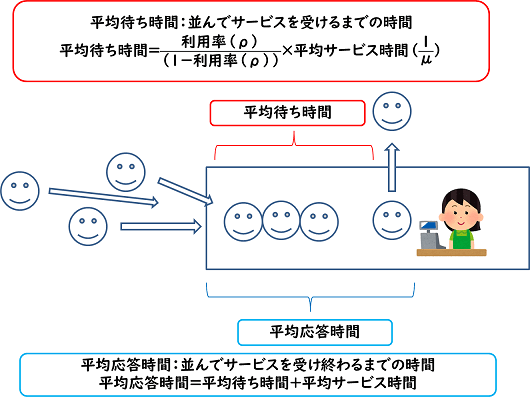
少し覚えるのが大変ですが、上記イラストをイメージしながら記憶していただけたら、と思います。
演習問題
実際の試験の過去問を解いてみましょう。
応用情報技術者試験 令和元年秋期 午前問3 問題
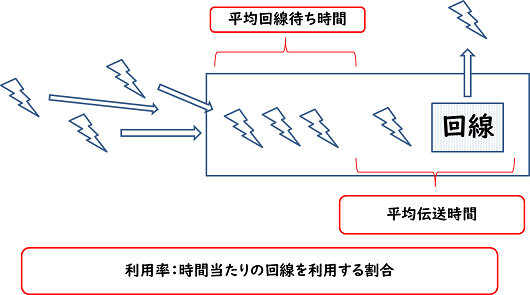
| IPA 応用情報技術者試験(AP) 問題より 問3 通信回線を使用したデータ伝送システムにM/M/1の待ち行列モデルを適用すると、平均回線待ち時間、平均伝送時間、回線利用率の関係は、次に式で表すことができる。  回線利用率が0から徐々に増加していく場合、平均回線待ち時間が平均伝送時間よりも最初に長くなるのは、回線利用率が幾つを超えたときか。 選択肢 ア 0.4 イ 0.5 ウ 0.6 エ 0.7 |
応用情報技術者試験 令和元年秋期 午前問3 解答
今回は事前知識不要で、文章の読解さえできていれば解けます。
「平均回線待ち時間が平均伝送時間よりも最初に長くなるのは、回線利用率が幾つを超えたときか」ということは、
超える境界値である
「平均回線待ち時間」=「平均伝送時間」
となるときの回線利用率を求めればよいということです。
つまり、以下のとおり回線利用率が「0.5」のときが境界値になります。

このことから、答えは「イ」であることが分かります。
なお、蛇足ですが
今回の問題はM/M/1の待ち行列モデルをネットワーク評価へ適用させたもので、前項の公式で紹介した
・平均待ち時間 = 平均回線待ち時間
・平均サービス時間 = 平均伝送時間
・利用率 = 回線利用率
に対応します。
待ち行列理論の解説は以上です。
こちらに他の応用情報技術者試験のまとめについて掲載していますので、
良かったらご覧ください。
当ブログ「応用情報技術者解答解説」まとめページはこちら


